Prode Properties
Properties of pure fluids and mixtures, multi phase equilibria, process simulation, software

Title : phase envelope, diagram, curve, curves, natural gas dew point, hydrate formation, Excel Matlab Mathcad software

Download
Download Prode Properties
Properties
Documentation, includes software installation and detailed description with application examples
Contact Prode
Do you need assistance or wish to discuss applications ?
Contact Prode

Prode Properties is the thermodynamic library created by Prode, it has been verified by Prode and other companies for more than 25 years of service, there are version for Windows, Linux, Android and client / server installations

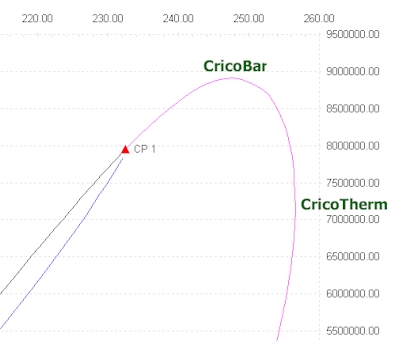
Application example : vapor-liquid-liquid phase envelope

Prode Properties can calculate different types of phase diagrams

Definitions

image

Server Side (Linux server) online application examples

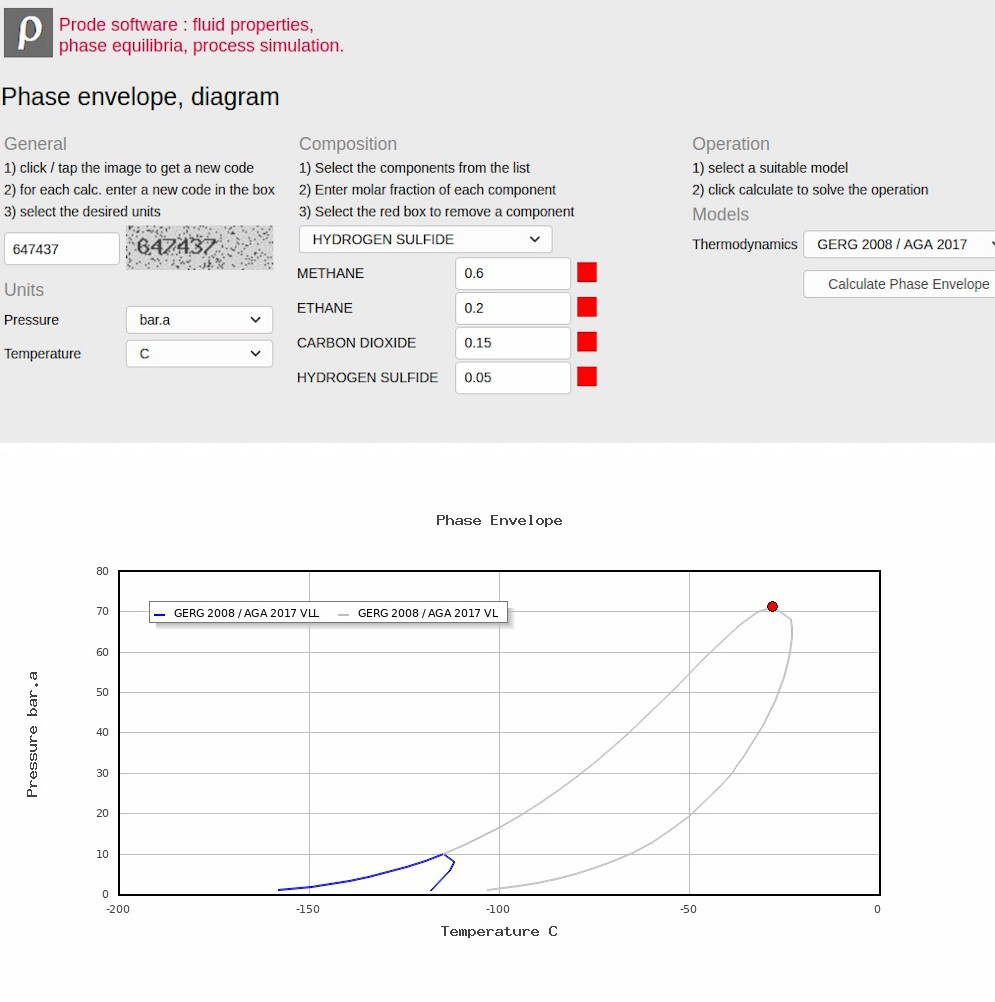
Local (Windows desktop) application example : create a phase diagram with Excel / Matlab / Mathcad

First step: define the stream (components, compositions etc.)

Properties includes a Stream editor which permits to access all informations (as compositions, operating conditions, models, options) for all streams which you need to define, to access the Stream editor from Excel Properties menu select Edit Properties

image

The Stream editor includes several pages, from the first page you can select a stream (Properties can store all the streams required to define a medium size plant) solve a series of flash operations and see the resulting compositions in the different phases, in this page select the stream you wish to define, for example the first.

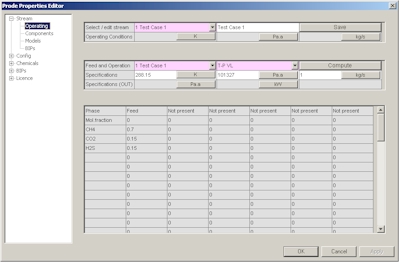
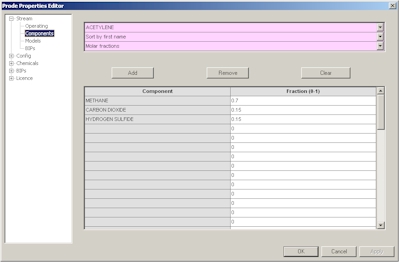
image

In the second page you can define a new composition or modify an existing composition, in this example we define C1 0.7 CO2 0.15 H2S 0.15 as molar fractions

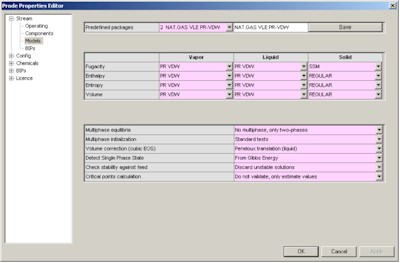
image

In the third page you can define the package (thermodynamic models and related options) , here we define API Soave Redlick Kwong.

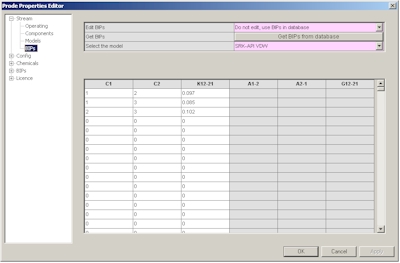
image

The fourth page provides access to BIP (Binary Interaction Parameters) for the different models, you can enter specific values or click on "Load BIPs" button to get the predefined BIPs from databank.

image

Finally we must save the new data, in the first page click on "Save" button, note that you can redefine the name of the stream as you wish (editing the cell near the button "Save"), you can define / modify many streams following the procedure described.
Once defined the stream you may wish to define the units which we wish to utilize in our problem, in stream editor go then to the "Units" dialog

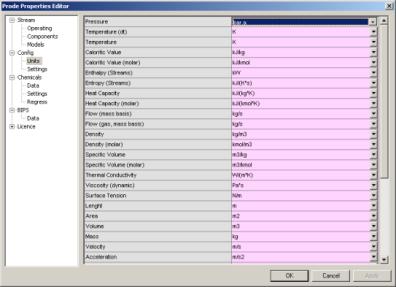
image

here you can select the units which you need for a specific problem, in this example for the pressure (first row) select Bar.a , notice that unit for temperature is K (but you can set the units which you prefer) then click on Ok button to accept new values and leave the Properties editor.
Now you are ready to use Properties for calculating all the properties which you need, however there is still a last thing to do if you do not wish to lose all data when leaving a Excel page, precisely to save data to a file, to save data to a file from Excel Properties menu select "Save a Archive"

image

then select the file "def.ppp" if you wish that Properties utilizes this data as default (this is the normal , recommended option), differently set a different name (you can for example define different names for different projects) but you will need to load that specific Archive before to make calc's for that project and since Excel reloads Properties with any new page this may result tedious...
Properties saves on the file also the units of measurement so you can define different streams and different units in different projects.

image

Now you can calculate all the properties which you need with the units which you prefer for all the streams defined in that project.

Second step: generate a vapor-liquid-liquid phase envelope in Excel.

For generating the phase envelope we?ll use a predefined Excel page distributed with Prode Properties, from Excel menu File->open , in Excel folder (Prode Properties installation) select the file phasenv.xls

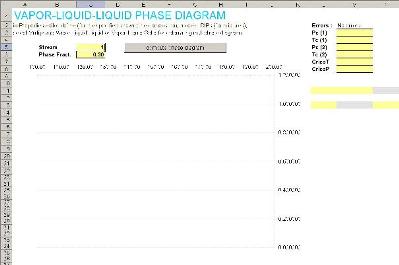
image

This page contains a little VBA code to tranfer the calculated equilibrium values (for the different vapor-liquid, liquid-liquid-vapor, vapor-liquid-liquid lines) from Prode Properties to Excel, if required you can easily modify the code for printing a series of lines with specified liquid or vapor fraction. To print a phase envelope you must define the stream (we select the first stream, which we defined with composition C1 0.7 CO2 0.15 H2S 0.15 , SRK as model and multiphase vapor+liquid option, the multiphase option instructs the procedure to generate a vapor-liquid-liquid phase envelope) we specify 0.3 value for liquid fraction, finally click on the button "calculate phase diagram".
Properties does all the work and the calculated equilibrium points including critical points, cricondentherm and cricondenbar are printed in Excel page for your analysis.

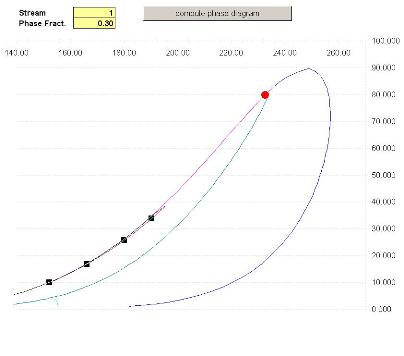
image

The phase envelope for this mixture shows a three phase area (notice the second line near the liquid-liquid-vapor bubble line and the third liquid-vapor-liquid line

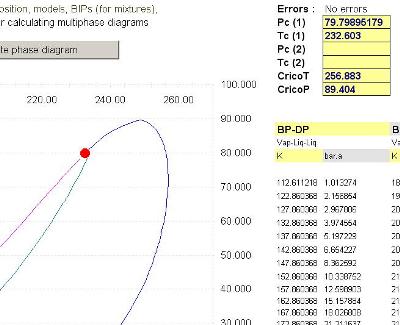
image

The calculated values for Critical Points, CricondenBar and CricondenTherm are available in Excel.
Note that Prode Properties calculates the TRUE critical points (not the estimated values), Prode Properties includes a proprietary procedure based on Gibbs minimization method.
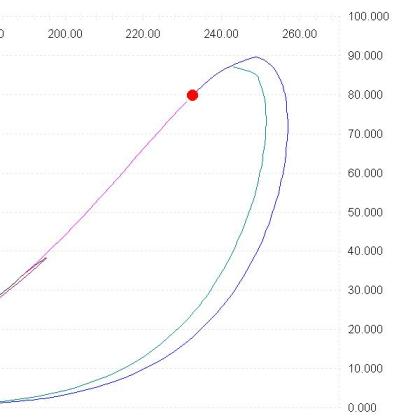
the procedure allows to specify any value (from 0 -dew line- to 1 -bubble line-) for phase fractions, herebelow the example of a line with 0.05 liquid fraction. image

The Vapor-Liquid-Liquid phase envelope constitutes the ideal tool to investigate the phase equilibria for mixtures of hydrocarbons + water
The example shows the phase envelope for a 12 components (hydrocarbons + water) mixture, notice the large three phase area where liquid water is present.

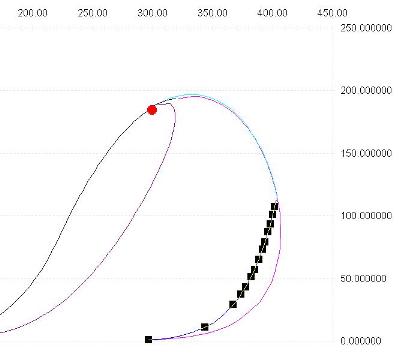
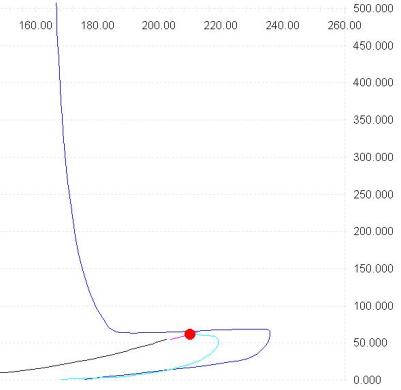
image

Note that even simple compositions can show a complex behaviour, herebelow is the example of the mixture with composition Methane 0.9 H2S 0.1 model API Soave Redlick Kwong.
The bubble line is a three phase (liquid-liquid-vapor) line, a vapor-liquid line connects the end of the liquid-liquid-vapor line with critical point, the dew line doesn't stop at critical point but continues, the blue line shows a liquid fraction of 0.05

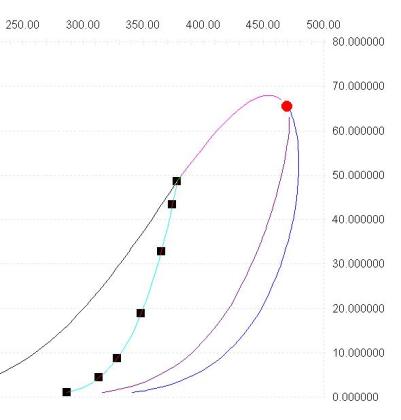
image image

Note that Prode Properties includes methods for calculating critical points, CricondenBar and CricondenTherm in Excel cells, see the paragraph "Methods for thermodynamic calc?s" in operating manual for the details.

To get the value of critical pressure enter the macro =StrPc(1,1) where (1,1) refers to the stream 1 and first critical point detected, we enter this macro in B1, in B2 we enter the macro =StrTc(1,1) to calculate the critical temperature in the same way, in cells B3 and B4 we enter the macros = StrCBp(1) for CricodenBar pressure and = StrCTt(1) for CricodenTherm temperature.

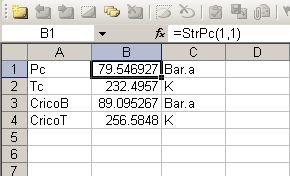
image

The phase envelope for this mixture (Methane 0.999 n-Butane 0.001) shows up to four saturation point pressures at the same temperature

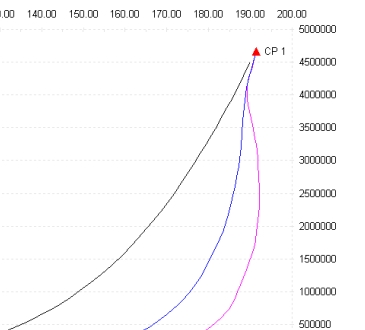
image

Observe the dew line, the red line below the critical point, there are up to three different equilibrium points at the same temperature (the area around 190 K), if you add the saturation point on the bubble line (black line) we have a total of four saturation point pressures at a given temperature, to calculate the points on the dew line we use the method:

double p = PfTF(integer stream, double t, double pf, int state, int n)

In cell B1 we define a value for the equilibrium temperature (190.208 K) , then in cells B2, B3, B4 we enter the macros

=PfTF(2,B1,0,1,1)

=PfTF(2,B1,0,1,2)

=PfTF(2,B1,0,1,3)

where the first value (2) is the stream which we defined, the second (cell B1) represents the temperature, the third (0) is the phase fraction (with 0 we specify 0% liquid or a point on dew line, the same would be by setting the state as gas and phase fraction as 1.0) the fourth (1) is the state (in Properties 0 = gas, 1 = liquid, 2 = solid) and the last is the required position (we require the points 1-3 along the dew line)

For additional infrmation about how to calculate equilibrium points go to the page Dew Points Natural Gas Hydrocarbons

Print a phase envelope in Matlab.

For calculating and printing the phase envelope we?ll use a predefined script distributed with Prode Properties, in Matlab command line type
>>phaseenvelope(1)
where (1) is the number of stream.

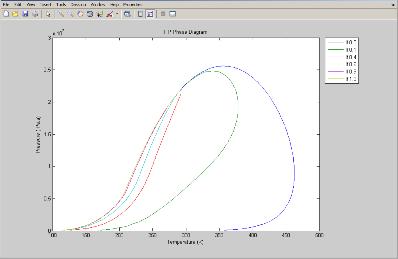
image

Prode Properties will calculate the phase envelope and print the result on Matlab, if you wish to obtain additional properties as cricondentherm, cricondenbar or critical points just enter the name of Properties method in Matlab, for example
>>StrPc(1)
will return the true critical pressure of stream 1.

Prode Properties, technical features overview (Windows version)

Typical applications